OBM e OBMEP
Lista 02, análise combinatória
Lista 01, análise combinatória
Construções Geométricas
Nas construções geométricas usaremos dois instrumentos:
i) Régua (ignoramos a graduação): usada para traçar retas, semirretas ou segmentos de retas, conhecidos dois pontos;
ii) Compasso: usado para traçar circunferências ou arcos e transportar medidas.
Construções Elementares:
1. Transportar um segmento de medida dada sobre uma reta.
Desejamos construir um segmento de medida $$ \overline{AB} $$ sobre a reta dada. Roteiro:
1. Assinale sobre a reta dada um ponto arbitrário $$ A_2 $$ .
2. Ponha a ponta seca do compasso em $$ A $$;e a outra ponta em $$ B $$ (ou vice-versa).
3. Com a abertura anterior, desenhe um arco com centro em $$ A_2 $$.
4. Marque a intersecção deste arco com a reta dada como ponto $$ B_2 $$.
5. O segmento $$ \overline{AB} $$tem mesma medida que $$ \overline{A_2B_2} $$. 2.
Transportar um ângulo de medida dada sobre uma reta.
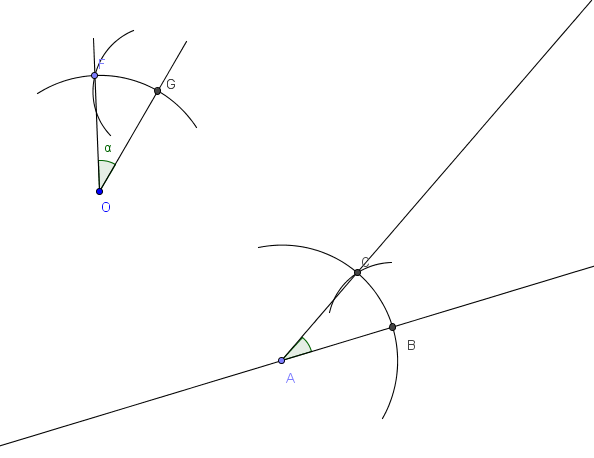
Desejamos construir um ângulo de medida $$ \alpha $$ com um lado sobre a reta dada. Roteiro:
1. Assinale sobre a reta dada um ponto arbitrário $$ A $$.
2. Com centro em $$ O $$ (vértice do ângulo dado) trace um arco de raio arbitrário que intersecte os lados do ângulo nos pontos $$ F $$ e $$ G $$ .
3. Com este mesmo raio, mas com centro em $$ A $$, trace um arco que intersecte a reta dada no ponto $$ B $$ .
4. Com centro em $$ B $$ , faça um arco de circunferência cujo raio mede $$ \overline{FG} $$.
5. Marque a intersecção dos arcos com centros em $$ A $$ e $$ B $$ como ponto $$ C $$ .
6. Desenhe a semirreta $$ \vec{AC}$$ .
7. O ângulo $$ C\hat{A}B $$ tem mesma medida que o ângulo $$ F\hat{O}G $$ .